Rechenschieber, Walzen und Scheiben Noch heute wird im Schulunterricht die Addition als das Anfügen von Strecken veranschaulicht.

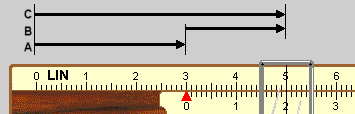
Die lineare Skala: A+B=C Im nebenstehenden Beispiel wird an die Strecke A=3 die Strecke B=2 angelegt. Das Ergebnis 5 kann unmittelbar abgelesen werden.
Nachdem Bürgl und Napier um 1600, unabhängig voneinander, die Logarithmen erfunden hatten, konnte die Multiplikation auf die Addition und die Division auf die Subtraktion zurückgeführt werden.
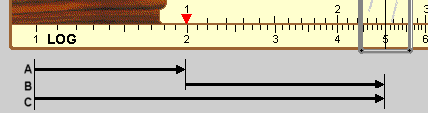
Die logarithmische Skala: A*B=C Hier wird an die logarithmische Strecke A=2 die logarithmische Strecke B=2,5 angelegt. Das Ergebnis 5 kann unmittelbar abgelesen werden.

Der englische Theologe Edmund Gunter berechnete 1620 eine logarithmische Skala, die in ein Messingplättchen graviert wurde. Die Werte wurden mit einem Stechzirkel abgelesen. Oughtred verwendete seit 1622 zwei aneinander gleitende, identische logarithmische Skalen.

William Oughtred (1574-1660)

Dieser Doppelstab bekam nach 1650 durch Wingate und Partridge die noch heutige übliche Gestalt mit einer „Zunge" die in einem „Körper" gleitet.

Nebenstehend einige typische Exemplare aus den Materialien Holz, Pappe, Metall und Kunststoff, wie sie bis ca. 1975 im Einsatz waren. Zusätzlich zu den logarithmischen Skalen enthielten sie meist noch quadratische, kubische, trigonometrische und Exponentialfunktionen und waren somit universelle wissenschaftliche Rechenhilfsmittel.

Dieses seltene Exemplar eines Drehbleistift verwandelt sich, wie im 2. Bild zu sehen, in einen vollwertigen Rechenschieber!

Rechenwalzen Die Genauigkeit des Rechenergebnisses eines Rechenschiebers ist um so größer, je größer seine Länge ist. Daher kam man auf die Idee, die Skalen schraubenförmig auf eine Walze zu wickeln.

	Otis King's Pocket Calculator
Dieses bekannte Exemplar einer Rechenwalze hat zusammengeschoben nur die Größe von 15 cm und kann also als echter Taschenrechner bezeichnet werden. Trotz dieser geringen Ausmaße hat die Skala eine Länge von 1,6 m!

Die Loga Walze   Die hier abgebildete Loga Rechenwalze aus dem Jahre 1930 hat bei einer Walzenbreite von 60 cm die Genauigkeit eines 15 Meter langen Rechenschiebers!

Rechenscheiben Eine Sonderform stellen die Rechenscheiben dar. Bei diesen sind die Skalen kreisförmig angeordnet.

Abwandlungen davon gibt es in allen Arten, Formen, Farben, Größen und für alle möglichen Spezialfälle. Hier z.B. der halbkreisförmige „Blumentritt's Metagraph" aus dem Jahre 1910 zum „Vergrößern und Verkleinern von Gefäßformen nach Längen und Hohlmaßen". Der Durchmesser beträgt 60 cm. Zum Größenvergleich eine Euro-Rechenscheibe.

	Die Euro-Rechenscheibe aus dem Jahr 1998 Dieses Werbegeschenk aus Pappe beweist, daß im Gegensatz zum Rechenschieber die Rechenscheibe auch heutzutage noch Anwendungen und Anhänger findet.

---

Rundgang

---

[ Homepage | Zurück | Inhalt | Anfang der Seite ]